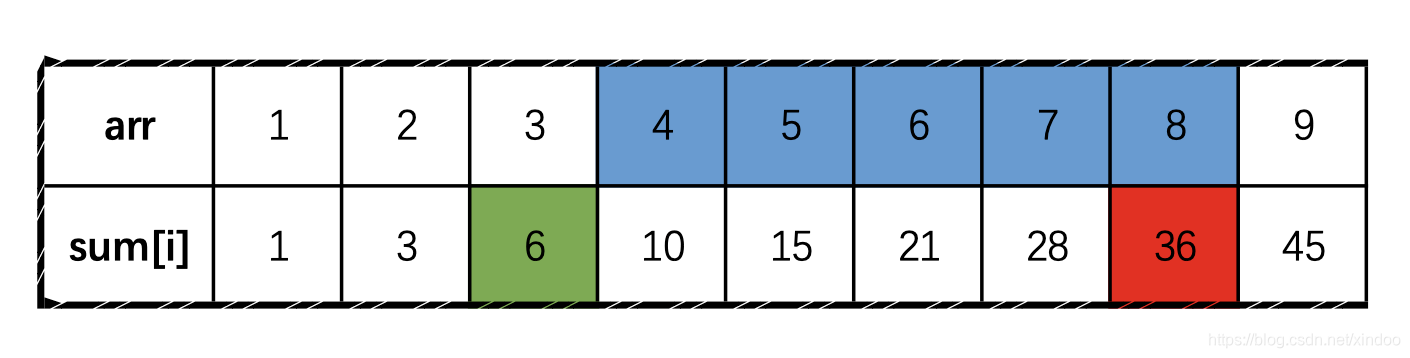
最开始学习机器学习的时候,首先遇到的就是回归算法,回归算法里最最重要的就是最小二乘法,为什么损失函数要用平方和,而且还得是最小?仔细想想最小二乘法视乎很合理,但是合理在哪,怎么用数学方法来证明它合理。
$$
J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2
$$
在真实数据中,一个x值可能对应多个y值,因为实际y值可能是受多种因素影响,所以我们可以假设任意一个x对于的y的真实值服从正态分布。我们什么时候可以认为模型$h_\theta(x)$ 拟合出来的点最好?当然是$h_\theta(x)$ 取值概率最大的时候。
如上图,红蓝两条线来拟合绿色的这些数据点,明显红色的直线拟合效果更好一些。为什么?仔细看图中直线上红色x点,红色的x点正好是当前x值下,训练数据中出现概率最高的位置(之前我们已经假设每个位置y值符合高斯分布)。所以我们要求的就是使得拟合出的线(高纬度是超平面)上概率最大的$\theta$,这个时候我们就可以用到极大似然估计。
接下来我们用极大似然来证明最小二乘法。假设误差$ε^{(i)} (1≤i≤m)$(就是上图中绿色数据点到红色x点的距离)是独立同分布的,服从均值为0,方差为某定值$\sigma^2$的高斯分布,我们可以得到似然函数。
$$
y^{(i)} = \theta^T x^{(i)} + \epsilon^{(i)}
p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\epsilon^{(i)})^2}{2\sigma^2}} \
p(y^{(i)}|x{^{(i)};\theta})= \frac{1}{\sqrt{2\pi}\sigma}e^{(-\frac{(y^{(i)}-\theta^Tx{^{(i)}})^2}{2\sigma^2})} \
$$
$$
\begin{equation}\begin{split}
L(\theta) &= \prod_{i=1}^m p(y^{(i)}|x{^{(i)};\theta}) \ &=\prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}e^{(-\frac{(y^{(i)}-\theta^Tx{^{(i)}})^2}{2\sigma^2})}
\end{split}\end{equation} \
$$
对上面似然函数求对数得到对数似然函数 $\ell(\theta)$
$$
\begin{equation}\begin{split}
\ell(\theta) &= logL(\theta) \
&= log\prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}e^{(-\frac{(y^{(i)}-\theta^Tx{^{(i)}})^2}{2\sigma^2})} \
&= \sum_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}e^{(-\frac{(y^{(i)}-\theta^Tx{^{(i)}})^2}{2\sigma^2})} \
&=mlog\frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{\sigma^2}\cdot\frac{1}{2} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2
\end{split}\end{equation} \
$$
上式中,$\sigma$ 是定值,我们要使得上式最大,就得使$\frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$最小,于是我们就得到了最小二乘。
$$
J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2
$$
其实通过这个公式我们可以求得关于$\theta$的解析解,可以直接计算出$\theta$,但我们一般不这么做,因为求解析解过程中需要求矩阵的逆,这是一个非常耗时的工作(时间复杂度$\Theta(n^3)$),另外矩阵也不一定可逆,一般都是用梯度下降。但我们还是看下如何求$\theta$的解析解。
$$
J(\theta) = \frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2
=\frac{1}{2}(X\theta-y)^T(X\theta-y)
$$
对$J(\theta)$求一阶导得到梯度。
$$
\begin{equation}\begin{split}
\nabla_{\theta} J(\theta) &= \nabla_{\theta} (\frac{1}{2}(X\theta-y)^T(X\theta-y)) \
&= \nabla_{\theta} (\frac{1}{2}(\theta^TX^T-y^T)(X\theta-y)) \
&=\nabla_{\theta}(\frac{1}{2} ( \theta^T X^T X \theta - \theta^T X^T y - y^TX\theta + y^Ty) ) \
&=\frac{1}{2}(2X^TX\theta - X^Ty - (y^TX)^T) \
&= X^TX\theta-X^Ty
\end{split}\end{equation} \
$$
因为$J(\theta)$是存在极小值的凸函数,什么时候取最小值呢?当然是梯度为0的时候。
$$
X^TX\theta-X^Ty = 0 \
X^TX\theta=X^Ty \
\theta = (X^TX)^{-1}X^Ty
$$
最小二乘法的极大似然解释
未经允许不得转载:XINDOO » 最小二乘法的极大似然解释